الزمكان في النظرية النسبية الخاصة ـ نظرة عامة ( الحلقة السابعة )
الزمكان في النظرية النسبية الخاصة ـ نظرة عامة
ملاحظة / يمكن تحميل كتب عن النسبية من هنا
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
فى الواقع فى النسبية لم يعد الزمان منفصلا عن المكان أبدا بل أصبح الزمان هو البعد الرابع بعد أبعاد المكان الثلاثة . و بذلك فقد أصبح تصورنا للكون الذى نعيش فيه هو أنه متصل رباعى الأبعاد يسمى الزمكان .
علينا أولا أن نعرف أنه عندما نرسم الزمكان و نتعامل معه هندسيا فإننا لن نرسمه رباعى الأبعاد – حتى فى أرقى الجامعات لا تتوافر صبورة رباعية الأبعاد – بل أنه اقصى ما يمكننا رسمه هو زمكان يتكون من بعدين مكانيين و بعد زمانى . فى الواقع من أجل التبسيط فسنتعامل مع عالم يتكون من بعد مكانى واحد و بعد زمانى . بينما تكون الأحداث فيه على شكل نقاط لكل منها إحداثيين واحد مكانى و الأخر زمانى .
حسنا و هكذا سيكون الخط العرضى هو x بينما الخط الطولى هو C t و هذه القيمة هى الزمن مضروب فى ثابت و هو سرعة الضوء هنا أما عن لماذا لم نجعله الزمن فقط و ضربناه فى سرعة الضوء فلا داعى للخوض فى هذا الموضوع الأن على العموم المهم فى الرسم البيانى هو مقياس الرسم و طالما ضربنا الأرقام كلها فى نفس الرقم الثابت فهذا لا يضر بصحة الرسم
خط السير
الأن لكل كائن أو نقطة فى هذا العالم خط سير او world line هذا الخط يحدد سيرها فى الزمكان . فمثلا المشاهد الثابت فى مكانه سيكون خط سيره موازيا للخط الطولى أى أنه يسير فى الزمن فقط بلا تحركه فى المكان ( لا تنسى أن كل مشاهد ثابت فى مناط اسناده ) الأن لو أنه هناك مشاهد بدأ يتحرك مبتعدا عن المشاهد الثابت فى اتجاه اليمين فكيف سيكون خط سيره فى مناط اسناد الثابت ؟ و ماذا لو تحرك فى اتجاه اليسار ؟ سيكون كما فى الرسم
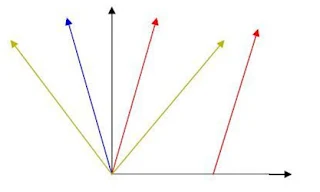
الخط الأحمر يوضح خط سير المشاهد المتحرك لليمين ، و الأزرق يوضح خط سير المشاهد المتجه لليسار بينما الأسود الطولى هو خط سير المشاهد الثابت . لو لاحظتم ذلك فإنه كلما زادت سرعة الجسم كلما قطع مسافة أطول فى زمن أقل مما يعنى أن خط سيره سينحرف مبتعدا أكثر عن الخط الطولى حتى يصل الأمر إلى سرعة الضوء .
فالخط الأصفر يوضح خط سير سرعة الضوء الذي يصنع زاوية 45 درجة مع الخط الطولى . تذكر أنه لا يمكن لجسم ما تجاوز سرعة الضوء أبدا أو حتى الوصول إليها . الخط الأحمر على اليمين هو خط سير مشاهد أخر أو جسم أخر انطلق بنفس سرعة المشاهد المسافر لليمين و فى نفس اتجاهه لكنه ابتدأ من نقطة بعيدة فى المكان . و بما أن له نفس السرعة فإنه ببساطة موازى للخط الأحمر الأول
بهذا نكون انتهينا من الخط الأول المهم و هو خط السير. تذكر أن كل مشاهد ثابت فى مناط اسناده و حتى الأن نحن لم نقدم شكل مناط اسناد المشاهد المتحرك الذى نرسمه .
البعد المكانى
الأن لكى تكتمل الصورة لا بد من تعريف الخط العرضى الذى نرسمه متعامدا على الإحداثى الزمنى . ببساطة هذا الخط هو الإحداثى المكانى أو مقياس المسافة . فى النفس الوقت يوجد وظيفة أخرى هامة لهذا الخط و هو أن جميع النقاط التى تقع على نفس الخط العرضى تحدث فى نفس الزمن أى متزامنة . يتضح الأن أنه لا بد أن يكون هناك خط عرضى مختلف فى مناطات الاسناد المختلفة و إلا فقدنا نسبية التزامن و هى النتيجة الأساسية للنسية الخاصة .
الأن و بدون اثباتات رياضية أو ما شابه فإن الخط العرضى للمشاهد المتحرك فى اتجاه اليمين أو فى اتجاه اليسار يتم رسمه كالأتى
واضح أن الخط العرضى ينحرف عن الخط العرضى للمشاهد الثابت بزاوية مساوية تماما للتى ينحرف بها الخط الطولى للمشاهد المتحرك عن الخط الطولى للمشاهد الساكن . و هكذا نكون قد رسمنا الزمكان بطريقة لا بأس بها واضح أنه بالنسبة للضوء ينطبق الخطين على بعضهما .
من الرسم السابق يتضح لنا أول شيئ يقدمه رسم الزمكان و هو أنه يعطى تخيلا جيدا عن ثبات سرعة الضوء فواضح أن النسبة ما بين الزاوية التى يصنعها خط سير الضوء مع الخط العرضى و الزاوية التى يصنعها مع الخط الطولى ثابتة لكل المشاهدين.
و الآن لنستعرض بعض الأشياء التى يساعد رسم الزمكان فى فهمها
تفسير الزمكان لانكماش الطول
هذا الرسم يوضح ببساطة تأثير نسبية التزامن على قياس الطول كما شرحنا سابقا .
تفسير الزمكان لتمدد الزمن
الآن سنأتى إلى واحدة من أهم النقاط الا و هى تمدد الزمن الذى وعدت بشرحه مرة أخرى فى صور جديدة .
و لنبدأ كلامنا بتجربة نظرية
لنقل أنك تسير بسرعة عالية منتظمة و عندما مررت بجانبى بدأ كلانا فى تشغيل ساعته . اعتبر أن سرعتك كانت تحدث تباطؤا فى الزمن بمقدار معين ألا و هو النصف أى أننى سأرى ساعتك دائما تقرأ نصف الوقت الذى تقرأه ساعتى .
هب أنه يمكننا أن نرى ساعات بعضنا البعض بأى وسيلة . الأن بعدما مرت ساعة على ساعتى (ساعتى تقرأ 60:00 ) سوف أنظر إلى ساعتك فلا بد و تبعا للنسبية أن أراها تقرأ 30:00 و لكن عندما تقرأ ساعتك هذه القرأة ستنظر أنت على ساعتى فمن المفروض تبعا للنسبية أن ترى ساعتى تقرأ 15:00 ، تعارض!!. السؤال هو عندما تقرأ ساعتك 30:00 فهل تقرأ ساعتى 60:00 كما أقول أنا أم تقرأ 15:00 كما تقول أنت ؟ ما هى قراءة ساعتى فعلا ؟!
ها قد ظهرنا بتحديا جيدا للنسبية و إذا فشلت فى تفسيره فستسقط النسبية فورا . لا بد انك تعتقد بوجود طريقة ما هنا للخروج من هذه الورطة . فعلا هناك شرح منطقى جدا و هو أنه لا يوجد أى تعارض فعندما تقول ساعتك 30 دقيقة فإن ساعتى تقول 60 فى مناطى بينما تقول 15 فى مناطك . اللعبة هى نسبية التزامن ففى مناطى يتزامن حدث قول ساعتك 30 دقيقة مع حدث قول ساعتى 60 دقيقة بينما فى مناطك فإن الحدث متزامن مع قول ساعتى
15 دقيقة . و دعونا نتأمل هذا الرسم الجيد فعلا .
هل رأيتم كيف يكون تمدد الزمن متبادلا . لعلكم لاحظتم شيئا غير مرضى فى الرسم . عندما قارن المشاهد الساكن قراءات الساعات فى المرة الولى رسم خطا عرضيا ليعرف ما هى قراءة ساعة المسافر الآن فى مناطه . و لكنه وجدها أقل منه . الشيئ غير المرضى هو أن طول الخط الطولى للمسافر من الأصل حتى هذه النقطة أطول من طول الخط الطولى للساكن (لأنه خط مائل) فكيف يكون قيمة وقت المسافر أقل إذن . حسنا إنها إضافة منكوفسكى الجبارة هى التى جعلت من الخط المتعرج أطول من الخط المستقيم عكس ما تعودنا دائما . أما ما هى هذه الإضافة فسنتكلم عنها لاحقا بعد شرح تحويلات لورنتز .
مفارقة التوائم فى الزمكان
بالطبع تمدد الزمن كما قلنا هو أعقد النقط من حيث التخيل . و ما زال هناك الكثير من التجارب النظرية لشرح هذه الظاهرة جيدا . و لكن لنعد إلى مفارقة التوائم
فى مفارقة التوائم ، لماذا يظل الأخ المسافر شابا بينما يشيب الأرضى ، ألا ينبغى أن يحدث العكس من
وجهة نظر المسافر ؟؟؟؟ مع العلم ان النسبية لا تفضل أى مشاهد على الأخر
الإجابة على هذا السؤال بسيطة جدا و لا تشكل أى تعارض للنسبية.
عندما ينطلق أحد الأخوين و ليكن أ و يبقى ب على الأرض . طوال رحلة أ ، سيرى ب أن وقت أ يسير ببطء و أنه عندما يعود سيكون أ أكثر شبابا .
من وجهة نظر أ ، ب هو الذى يتحرك و بذلك يجب أن يكون ب أكثر شبابا عند العودة.
سنرى أن وجهة نظر ب هى التى ستحدث و ذلك لانه لكى يعود أ عليه أن يغير سرعته ليتباطأ ثم يلتف ثم يتسارع مرة أخرى و بذلك هو خارج حسابات النسبية الخاصة لأن مناط إسناده ليس قصورى .
و لكن دعنا نتفادى هذه النقطة و نقول أن أ قفز فجأة من سرعته (س) إلى (-س) بلا تباطؤ أو تسارع.
فى هذه الحالة لا يمكن ل أ ان يدعى أنه مازال ساكنا لأنه سيجد الأشياء معه فى السفينة تغيرت حالتها كما تفرمل السيارة فجأة.
سيرى أ فى هذه اللحظة زمن الأرض يقفز قفزة كبيرة و هذا بسبب أن فى مناط إسناد أ القديم كانت نقطة التفافه متزامنة مع نقطة ما حيث أخوه مازال شابا و لكن فى مناط إسناده الجديد تتزامن نقطة التفافه مع نقطة ما حيث أخوه عجوز. و هذا راجع لنسبية التزامن.
و كلما التف على بعد أكبر كانت القفزة فى زمن الأرض أكبر و بذلك مهما تباطأ زمن الأرض بالنسبة لـ أ فى رحلة الذهاب و العودة فإن القفزة فى زمن الأرض كافية لتحقيق تنبؤ النسبية الخاصة.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
سجل إعجابك بصفحة الفريد على الفيس بوك ، وشارك زملاءك من الزر أدناه لتصلكم مواضيعنا القادمة إن شاء الله تعالى